
Mi normális, mi nem?
„Azért jöttem ide önökhöz, hogy elmondanám, hogy mi hülyeség és mi nem az” – mondotta volt mindannyiunk nagy mentora, aki ez alkalomból a tekintélyt és hitelességet sugalló Besenyő M. H. J. M. István, azaz Besenyő Minden Hülyeséget Jól Megmondó István nevet viselhette volna.
Itt az ideje azt is megtudnunk, hogy mi normális és mi nem. Persze ennek az lenne a legkönnyebb módja, ha fognánk a világegyetemet és kivonnánk belőle, ami hülyeség, tehát megmaradna a normális. „Ugye? Igen. Hát nem? De!” – mondaná erre valószínűleg a fentebb is idézett orákulum.
Ennél kevésbé komoly bejelentkezés is történt a normalitás meghatározására: „Normális ember normális társadalomban a természeti törvényeket figyelembe véve tudja, hogy mi normális” – idéz egy nyilvános Facebook-hozzászólást prof. Nagy Beáta: itt éppen egy polgármester szólt hozzá egy tudományos kérdéshez.
Önkéntelenül eszembejut Karinthy Frigyes véleménye, amely szerint megkérdezhetünk művészeket [és hozzáteszem: tudósokat]; és megkérdezhetünk politikusokat. A művészek [hozzáteszem: és a tudósok] megfontolt, felelős, őszinte véleményt mondanak, míg a politikusokkal kapcsolatban efelől kétségeink lehetnek. Nyilvánvaló, hogy kit érdemes megkérdezni: a politikust – mondja Karinthy, „mert a művész [hozzáteszem: és a tudós] azt mondja meg, hogy minek kellene lennie, de azt én is tudom; a politikus viszont azt mondja meg, hogy mi lesz”.
A teendő egyszerű: ha kíváncsiak vagyunk, mi normális, csak megkérdezünk egy normális társadalomban élő normális embert: ő tudni fogja. A kérdés csak az, hogy mielőtt őt meghallgattuk arról, hogy mi és ki a normális, vajon hogyan állapítjuk meg, hogy melyik a normális társadalom és ki az a normális ember, akit megkérdezhetnénk. Kicsit olyan ez, mint a bezárt láda, amelyikben benne van a kulcs.
Nem könnyű itt eligazodni: egyáltalán nem vagyok biztos abban, hogy ha találkoznának mindazok, akiknek ilyen pontos és határozott véleményük van a normalitásról, akkor legalább ők ugyanazon a véleményen volnának.
Hadd forduljak a leginkább egzakt tudományhoz, a pontosság gondolkodási etalonjához, a logikus gondolkodás non plus ultrájához: a matematikához, abban a reményben, hogy az Olvasó erre felsóhajt: no végre; olyan régen olvastam valami jó kis matematikai gondolatsort. Hát akkor íme.
A valószínűségszámításban jól ismert a „normális eloszlás”, amelynek az ábráját Gauss-görbének, harang-görbének is nevezik.
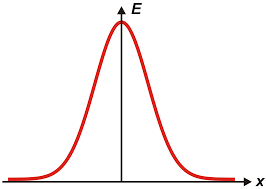
Ennek az az érdekessége, hogy ha olyan jelenséget, helyzetet vizsgálunk, amelyet semmi nem torzít, akkor párezer adat esetében szinte bizonyosan normális eloszláshoz jutunk, legyen szó emberek intelligencia-hányadosáról vagy cipőméretéről, olvasási sebességéről vagy várható élettartamáról: szinte akármiről.
Egy példa a matematikai definíciókat kevésbé kedvelő Olvasónak: ha a testmagasságot az óvodában mérem, akkor két „csúcs” lesz: egyik az óvodások átlaga, másik a gondozóké; éppen úgy, mint ha az életkori megoszlást az idősotthonban mérem vagy a gyermekotthonban. Ilyenek azok az esetek, amikor a minta összetétele nem független attól, amit mérni akarunk.
A harang-görbét nemcsak az jellemzi, hogy hol a csúcsa, hanem az is, hogy mennyire csúcsos vagy lapos:
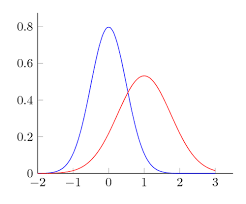
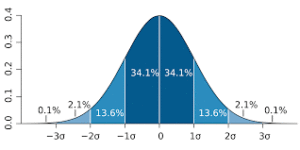
Akit mégis érdekel a számolás módja: tegyük fel, hogy megmértük 5 ember magasságát és a következő értékeket kaptuk: 174, 169, 178, 174, 170 cm. Ezeknek az átlaga (174+169+178+174+170)/5 = 173 cm. Most az egyes értékeket sorra kivonjuk az átlagból és ezeket a különbségeket négyzetre emeljük, az így kapott értékeket pedig összeadjuk: (173-174)² + (173-169)² + (173-178)² + (173-174)² + (173-170)²= (-1)² + (4)² + (-5)² – (-1)² + (3)² = 1 + 16 + 25 + 1 + 9 = 52. Az eredményt elosztjuk az adatok számánál eggyel kisebb számmal: 5 adatunk van, tehát most néggyel osztunk: 52÷4 = 13. A fenti számsorozatnak ez a szórása. Figyelem: az 5 adat messze nem „statisztikai sokaság”! Ha ennyi adattal példálózunk, ez semmit nem cáfol és semmit nem bizonyít!
Ha valami normális eloszlású, akkor (kis kerekítéssel) az adatok 68%-a az átlagtól legfeljebb szórásnyi távolságra van, az adatok 96%-a átlagtól legfeljebb kétszeres szórásnyi távolságra, az adatok 99,8%-a átlagtól legfeljebb háromszoros szórásnyi távolságra. Akkor is, ha intelligencia-hányadosról vagy cipőméretről van szó, és akkor is, ha olvasási sebességről vagy várható élettartamról: bármiről, ami normális eloszlású.
Ha például egy (megfelelő méretű, nem pedig a fentebb példaként látható ötelemű!) adatsorozat átlaga 173 és a szórása 13, akkor az adatok 68%-a (körülbelül kétharmada) 160 és 186 közé esik (azaz 173-13 és 173+13 közé); az adatok 96%-a 147 és 199 közé esik (azaz 173-2×13 és 173+2×13 közé).
Átlag ± szórás: ez a tartomány lefedi az adatok kétharmadát; átlag ± kétszeres szórás: ez a tartomány pedig lefedi az adatok 96%-át.
Mivel pedig ha olyan jelenséget, helyzetet vizsgálunk, amit semmi nem torzít, akkor párezer adat esetében szinte bizonyosan normális eloszláshoz jutunk, ez az emberek minden olyan tulajdonságára és tevékenységére is igaz, amelyet megfelelően független referenciacsoportokkal mérni tudunk: a vásárlási szokásokra és az házasélet adataira, időbeosztásra és személyiség-jellemzőkre, választási preferenciákra és értékrendre, társadalmi kérdésekben való aktivitásra és egészséges étkezésre. Mindenre, amit úgy tudunk mérni, hogy a mérés céljától független módon választott, megfelelően nagy csoport kellőképpen sorbarendezhető adatait kapjuk.
Mély lélegzet, lazítás: az összes ilyen kérdésben tehát a népesség egyharmada van csak szórásnyi mennyiségnél távolabb az átlagtól, a népesség 4%-a van csak kétszeres szórásnyi mennyiségnél távolabb az átlagtól.
Átlag ± kétszeres szórás: ez 96 százalék: ha Magyarország népességét kerekítve tízmilliónak számoljuk, akkor ebből 200.000 ember „lóg ki” az egyik oldalon, ugyanennyi a másikon. Feltehetően ennél nagyobb a csecsemők és a magatehetetlenek létszáma… és vannak emberek börtönben is és kórházban, elmegyógyintézetben, a Parlamentben… vagyis vannak, akik nem a „mindennapi emberek” életét élik, nem a „mindennapi élet” szabályai vonatkoznak rájuk: mások a lehetőségeik, más korlátozza őket. Amikor arról beszélünk, hogy mi jellemzi az adott társadalomban élők életét, őket nyugodtan kihagyhatjuk. Kétségtelenül a társadalom tagjai, de amikor jellemezni akarjuk a társadalmat, nem róluk van szó. Ha arról beszélünk, hogy adott társadalomban hogyan élnek az emberek, melyek az adott társadalom „játékszabályai”, akkor bizony ebből a szempontból az „átlag ± kétszeres szórás” tartomány maga a társadalom.
Átlag ± szórás: ők pedig a normálisak.
A teljes létszám 68%-a van az átlagtól legfeljebb szórás-mértékű távolságra: ez kétharmados többség, mégpedig igazán a teljes populáció (a felmért népesség, csoport) kétharmados többsége. Nekik szólnak – ha „mindenkihez” akarnak szólni – a napilapok és az árleszállítások, a tévéműsorok és az azokban megjelenő reklámok; őrájuk tervezik a konfekcióruhákat és a menetrendeket, a szupermarket polcain az áruk elrendezését. Ők a normálisak, mert az ő viselkedésük a megszokott, az általános, a norma. Minden korban, minden társadalomban ezt a többséget, ezt a tömeget tekintették normálisnak, és az számított különcnek, deviánsnak, rendetlennek, rendbontónak, érthetetlennek, vagy csak egyszerűen „másmilyennek”, aki nem ilyen volt.
Aligha tudunk olyan furcsaságot mondani, amelyik valahol ne számítana vagy valamikor valahol ne számított volna „normálisnak”, etalonnak, követendő mintának, életmódbeli és viselkedési normának: a Szilíciumvölgyben vagy a Neandervölgyben, az ókori távolkeleten vagy Leszbosz szigetén, az eszkimóknál, az inkáknál vagy azoknál, akik még inkább. (Pardon.) De olyasmit is nehéz mondani, amilyen viselkedés, életmód valamikor máskor, valahol másutt ne számított volna „másmilyennek”: szerencsés esetben csak furcsának, de másutt talán megvetettnek, kiközösítettnek vagy elpusztítandónak.
Van-e ezek közt „rangsor”? Van-e, ami „abszolút normális”, vagy legalább „normálisabb”? Úgy érezzük, hogy igen – de a jó kutatót nem befolyásolhatja, hogy mit sejt a kutatása majdani eredményéről.
Térjünk később vissza erre; most pedig befejezésül hadd idézzem (sokadszor) az egykori kedvenc geometria-tankönyvem egyik lábjegyzet-mondatát: „Mi csak megmagyarázzuk álláspontunkat, de nem állítjuk, hogy ez az egyetlen lehetséges álláspont.”














