Gyönyörű tavunk, a Balaton vízfelülete 592 km². Nagyobb egész Andorránál, 3,7-szer nagyobb, mint Liechtenstein, Máltának majdnem kétszerese, nem is említve Tuvalut, Gibraltárt vagy Vatikánt: ötvennél több ország van, amely elférne Balaton-méretű területen. Ez Közép-Európa legnagyobb tava (amiben persze szerepe van az egyes- és többesszám megfelelő használatának, amely miatt a majdnem kilencvenszer-ekkora Mazuri tóvidék nem egyetlen tónak, hanem különálló tavak sokaságának számít – pedig hajóztam rajta úgy, hogy a hajó reggel indult és késődélután még mindig ugyanabba az irányba ment, a külön tavak sorának számító, de egybefüggő vízen).
Jó nagy, no. A 236 km hosszú partszakaszon nemcsak üdülők, strandok, vitorlástelepek és szállodák vannak, hanem idilli kis szakaszok is, nádassal, partig húzódó fás területtel: mintha érintetlen természetet látnánk.
Tegyük fel, hogy van egy gonosz vízinövény, algafaj, űrlény, akármi, amelyik hopp, fogja magát és ellep, a levegőtől elzár a vízfelszínből valamennyit: egy kisebb lábnyom méretével azonos felületet: másfél-két négyzetdecimétert. Legyen a példa kedvéért egy és háromnegyed dm². Hűha! A vízfelszín 0,000000003 százaléka!
Észre sem vesszük, ha az orrunk előtt van gumimatracozás közben, akkor sem.
Ez a gonosz valami viszont szaporodik. Megduplázódik – naponta.
Hát szaporodjon. Miért is ne lenne meg neki is ez az öröme?
Egy nappal később már 3½ dm²: nem semmi, ugye? Hát de. Ha foszforeszkálna és kiabálna, akkor se vennénk észre már a túlpartról se, még ott sem, ahol a tó a legkeskenyebb.
Ahogy telnek a napok, az ellepett vízfelület 7, 14, 28 dm² lesz: hét nappal a szennyeződés első megjelenése után 224 dm². Ez már több mint két négyzetméter: tekintélyes méret: egy franciaágy felületénél is alig kisebb… 0,00000038% a tó felszínéből – bolond, aki ettől megijedne.
Az meg csak ott röhög magában és szaporodik tovább.
Négy és fél négyzetméter, aztán kilenc… eltelik még egy hét. A vízfelszínen majdnem 300 m² trutymó úszik: körülbelül a balatoni átkelőhajók fedélzet-területének a kétszerese. Ez már jól látható – node ha van egy akkora méretű folt valahol a vízen (a vízfelszín nem egész fél ezred ezrelékén): ki figyelne fel rá, ki tulajdonítana fontosságot neki?
Ugyan már: még a harmadik hét letelte után sem láthatunk igazi bajt. A tófelszín alig több mint fél század-százalékán úszik valami izé: ha fogná magát és egyetlen csíkba rendeződne a Balaton hosszában, annak a csíknak a szélessége a fél métert se érné el: ahogyan a fodrozódó vizet nézzük elmerengve, fel sem tűnik a (magában) röhögő veszedelem.
Eltelnek a következő napok is, itt a negyedik hét vége: 28 nappal vagyunk a furcsaság megjelenése után. Az általa lefedett vízfelület majdnem félmilliárd dm² (csak a pontosság kedvéért: 469.762.048 dm²): ezt nehéz lenne tenyér-méretben, fürdőkádban vagy vitorla-felületben kifejezni… Ez az 4,7 km² már feltűnő. A Keszthelyi Öbölnek úgy hatodát foglalná el (ezt nem tudom pontosan kiszámolni, mert az öböl mérete más és más számítások szerint 25 és 39 km² közötti). Ha tehát ott gyűlne össze ez az egész, akkor biztos, hogy felfigyelnének rá. De ha eloszlana a tó egész felületén, amelyhez képest nem egész 1%: pánikkeltőnek tartanák az, aki rémüldözne. Esetleg megjelenik egy újsághír, hogy piszkos a tó vize, esetleg megjelenik egy hír arról, hogy reklamáltak az üdülővendégek. Egy-egy hozzáértő szakember azonban már valószínűleg felfigyelt, és elhatározta, hogy másnap utánanéz.
31 nap, egy teljes hónap telt el a veszedelem lábnyom-méretű megjelenése óta: a terjedelme 37,6 km², vagyis a Keszthelyi Öböl már eltűnne alatta. Ha azon a helyen koncentrálódik ez a szaporodó valami, akkor ott már pánik van. Ha eloszlik, ez még mindig csak a tó-felszín nem egész 6½ százaléka: nem egész tizenötöd része. A hozzáértő szakember már ebből is látja, hogy baj van: sürgős feljegyzést ír a felettesének.
Erich Kästner remek könyvében május 35 napból áll: nézzük, mi a helyzet harminckettedikén, amikor a felettes elé kerül a feljegyzés. Ő valószínűleg csak akkor tulajdonít fontosságot az ügynek, ha rájön (vagy a feljegyzésben szerepel), hogy aznapra már majdnem 13%, másnapra pedig – ha így halad tovább – több mint 25% az ellepett tó-felület.
Tegyük fel a legjobbat: másnapra sikerül válságstábot összehívni, ahol minden döntéshozó jelen van és mindenki érti a helyzetet. Tegyük fel, hogy azonnal elvégeztetnek egy légifelvétel-alapú mérést: igen, 25,39%, 150 km². Tegyük fel, hogy látják, hogy azonnal intézkedni kell (vagyis hogy azt hiszik, hogy még lehet intézkedni): másnapra kivezénylik a katasztrófa-elhárítókat, a katonaságot, mindenkit, aki segíthet.
Itt a másnap: harmincnegyedike. Több mint 300 km² a lefedett vízfelület: a tófelület 50,8 százaléka – és mire letelik az Erich Kästner-féle 35-napos hónap, a Balaton eltűnt.
Nem értek hozzá: nem tudom, hogy hányadik az a nap, amikor a halak kipusztulnak, amikor már a fürdőzőkre is veszélyes a helyzet – de ezek az időpontok valahol ott vannak a huszonnyolcadik és a harminckettedik nap között. A huszonnyolcadik napon a kezdettől a tó eltűnéséig tartó idő négyötöde már eltelt, és még csak a vízfelszín nem egész 1 százalékán látszik (ha látszik) valami szokatlan; és már csak az addig eltelt idő egyhetede kell ahhoz, hogy a szakember számára feltűnjön, és annyi sem, hogy végetérjen a tó teljes pusztulásával.
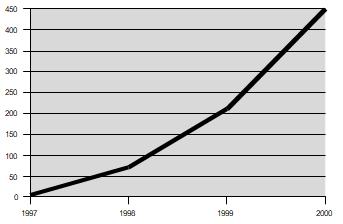
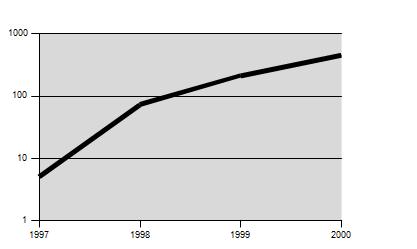
Ez a mértani sorozat aljas trükkje. A mértani sorozat (amikor időközönként, lépésenként, ütemenként nem azonos mértékben, nem azonos mennyiségben, hanem mindig azonos arányban változik valami) hosszú szakaszon „láthatatlan”, és a laikus nem is sejti, hogy mennyire „beindul” majd.
Ugyanez a lényege annak a közismert legendának is, amelyben a sakkjáték feltalálója jutalmul egy búzaszemet kért a sakktábla első mezőjére, kettőt a másodikra és így tovább; és a kérésbe óvatlanul beleegyező szultán nem jön rá időben, hogy a 64. mezőre kívánt 263 búzaszem a Föld egész búza-termésénél is több. Csak arra gondoltam, hogy ugyanez a történet a Balatonnal elmesélve érzékletesebb, mintha búza-hombárokat képzelünk egy sakktáblára.
Ugye nem kell kisiskolás módon, szájbarágósan leírnom, hogy hogyan működik ugyanez a jelenség a bankbetéteink és a hiteleink kamatos kamata esetében: hogyan növekedhet szerény befektetés is az embert eltartani tudó passzív jövedelemmé és hogyan taszíthat csődbe és nyomorba a látszólag alacsony kamatozású hitel? (Kelleni nem kell, de célszerű lehet. Fent van a terveim listáján.)
Most jól jönne valami frappáns befejező mondat; de inkább hadd hívjam fel a figyelmet arra, hogy az Új noteszlap az adatról látványos példát tartalmaz, hogy hogyan manipulálható a benyomásunk azzal, ha egy adatsort a mértani sorozat szemléletével mutatunk be.